Программа курса
Задание 1. Упростить выражение
Для решения этого примера понадобится знание формулы суммы кубов и умение приводить дроби к общему знаменателю.
Задание 2. Последовательное применение скидок
Необходимо найти последовательность действий, которые приведут к большей итоговой скидке, и определить, сколько она составит в каждом случае.
Задание 3. Составить неравенство, используя словесное описание данных
Необходимо решить задачу с применением формулы, имея исходные данные.
Задание 4. Решить уравнение с корнем
Опасная ошибка – сразу сократить скобку, что неизменно приведет к потере корня.
Задание 5. Решить уравнения
Необходимо решить уравнение с помощью замены переменной.
Задание 6. Решить неравенство с модулем
Задача имеет несколько вариантов решения.
Задание 7. Решить кубическое неравенство
Опасная ошибка - сокращение на х!
Задание 8. Использовать теорему Виета при решении уравнения
Выразить квадрат разности корней через квадрат суммы и произведения корней.
Задание 9. Построить график функций
Выражение под модулем разложить на множители.
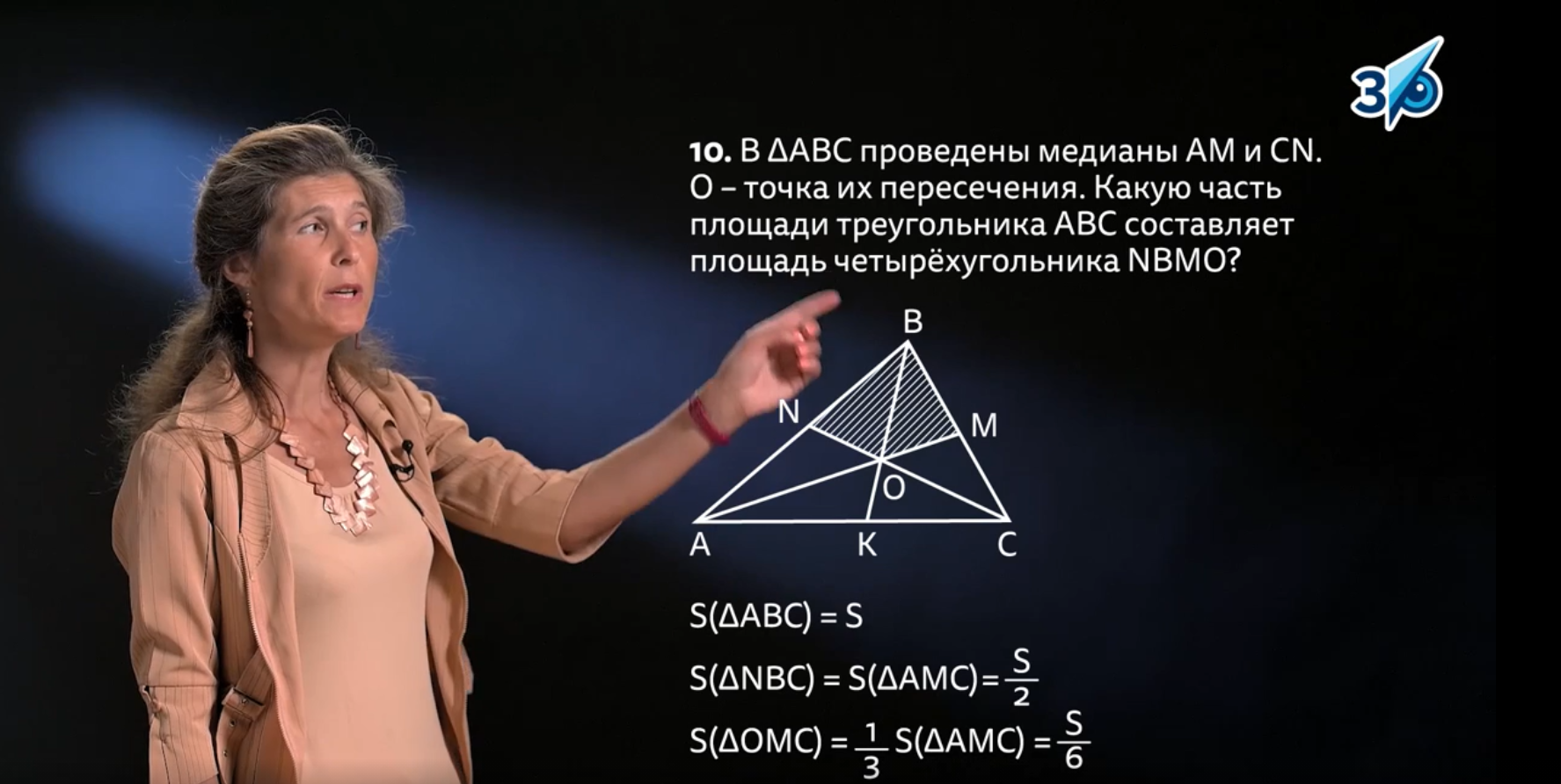
Задание 10. Решить геометрическую задачу, касающуюся вычисления площади треугольника
Здесь необходимо вспомнить о том, что если треугольники опираются на общую высоту, тогда их площади относят так же, как их основания.
Введение в курс
Преподаватели
Гнедина Ирина Сергеевна
Преподаватель математики ГФМЛ №30
Соросовский учитель
Учитель высшей категории
Эксперт ЕГЭ по математике