Задачи на построение и окружность
Соединение двух тем геометрии, традиционно вызывающих у школьников существенные трудности: «Задачи на построение» (7-8 класс) и «Окружность» (8 класс).
Преподаватели: Екатерина Викторовна Осипова
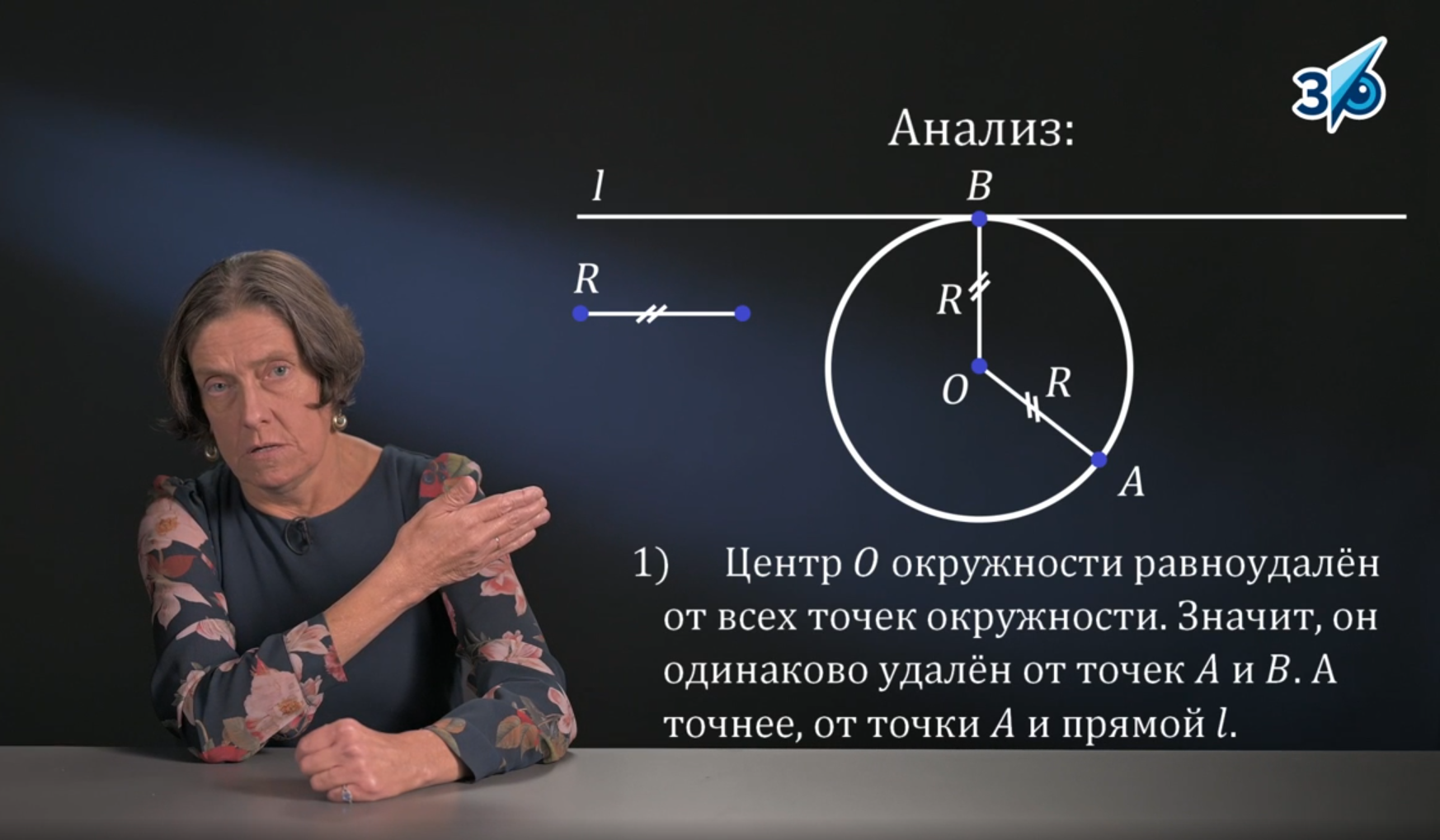
Соединение двух тем геометрии, традиционно вызывающих у школьников существенные трудности: «Задачи на построение» (7-8 класс) и «Окружность» (8 класс).
Преподаватели: Екатерина Викторовна Осипова

Из всех школьных, да и не только школьных, математик, геометрия является, пожалуй, самой наглядной, аксиоматичной, иллюстративной и доказательной. Для ребят, особенно привыкших за предыдущие годы обучения «подставлять числа в формулу», все эти связки довольно трудны. Если в задаче надо найти числовое значение длины отрезка, площади треугольника, тригонометрической функции угла или чего-то еще, зачастую ее превращают в расчетную, где с ходу начинают проводить всякие, даже, возможно, формально правильные, алгебраические вычисления. Не заботясь о том, почему мы можем делать такие преобразования именно здесь, в этой модели. Какая здесь теоретическая основа. Верно ли нарисована картинка, то есть понята сама модель. Да и вопрос о разрешимости задачи и количестве возможных случаев является не всегда тривиальным.
В задачах на построение, в силу их специфики, все эти вопросы естественным образом выходят на передний план, побуждая ребят задумываться над глубокой структурой и внутренней сутью задач. Благодаря этому яснее становятся свойства фигур, их взаимосвязи, явные и скрытые, задачи начинают играть новыми красками, проявляясь как бы «изнутри».
В школьной программе геометрии, которой придерживается подавляющее большинство школ, тема «Построение циркулем и линейкой» появляется примерно в середине 7 класса, и может снова возникнуть в конце его, в рамках построения треугольника по трем элементам. Возможно, еще кусочек в 8 классе, применительно к построению параллелограмма и его родственников. Но, как показывает опыт, на практике она очень быстро пробегается или пропускается вовсе. Что и понятно, ведь школьному учителю на геометрию отводится крайне мало часов. Тогда как именно она является прародительницей современной математики. А если разобраться, то именно ее задачи на построение. Тема «Окружность» приходится на конец 8 класса. И тоже является довольно многострадальной. То ее практически не успевают обсудить из-за того, что весной пропадает много уроков. То успевают самый минимум, не до красоты.
Также у детей 7-8 класса еще природно невысокий уровень абстракции мышления в силу возраста. Поэтому в данном курсе мы предлагаем приобщиться к красоте задач на построение всех старших школьников.
Этот курс создан для школьников 8-11 классов. Прежде всего для тех, кто хотел бы лучше подружиться с такими непонятными задачами на построение.
Регистрируйтесь и выбирайте курс — он сразу появится в вашем личном кабинете
Проходите уроки курса, смотрите видео и дополнительные материалы
В курсе нет дедлайнов: можно начать учиться в любое время и выбрать удобный темп
Это вводный урок. На нем мы обсудим важность и значимость задач на построение, идею формирования и примерный план всего курса. Затем мы перейдем к основной сути этих задач и их составляющим, обсудим инструменты, используемые при их решении, – циркуль и линейка. После перейдем к этапам и методам решения, перечислим «базовые» задачи на построение, которые традиционно берем в более сложных задачах, как понятную и известную основу. Завершим урок 1 рассмотрением сути метода ГМТ и трех основных ГМТ, тоже берущимся впоследствии за некую основу.
Здесь мы плавно продолжим начатый разговор о методе ГМТ. Затем, используя аксиоматику геометрии и метод ГМТ, поэтапно и подробно расскажем о решении некоторых базовых задач, перечисленных на первом уроке: 1. отложить отрезок, равный данному, на данном луче; 2. отложить угол, равный данному, в данную полуплоскость; 3. построить серединный перпендикуляр к отрезку; 4. построить прямоугольный треугольник по катету и острому углу.
Этот урок полностью посвящен взаимодействию задач на построение с окружностью. Тема «Окружность» и все, что с ней связано, обычно непросто дается детям. Видимо, отчасти оттого, что наш мир довольно линеен и угловат, на поверхностный взгляд. Окружностям в нем мало места. Поэтому мы начнем с задачи «Построить окружность по трем точкам», неожиданной для многих ребят. Свяжем окружность с треугольником, вспомним вписанную и описанную окружности. И естественным образом перейдем ко второй задаче: «Построить касательную к окружности с данным центром данного радиуса, проходящую через данную точку».
На этом уроке будут рассмотрены три задачи, решаемые, в том числе, при помощи тех самых «базовых» задач, о которых шла речь на Уроках 1 и 2. И первая из них является, в некотором роде, обратной к задаче, решенной на уроке 4: «Постройте окружность данного радиуса, касающуюся данной прямой в данной точке». Такое рассмотрение одних и тех же объектов с разных сторон помогает уйти от слепого заучивания к пониманию истинной природы изучаемых объектов и их взаимосвязей. Вторая задача обманчиво звучит похоже, однако предполагает совсем другие идеи. Здесь напрямую реализуется подход, описанный в курсе «Мы ТАК учим». И третья задача для ребят совсем уж внезапна. Она начинается со слов «На плоскости дана окружность, центр которой неизвестен…». Как так, неизвестен? Как же быть? Искать. Нет безвыходных ситуаций, и мы это увидим в решении третьей задачи.
На прошлых уроках была проведена большая подготовительная работа, и теперь мы можем перейти к рассмотрению более сложных закономерностей и задействовать более широкую теоретическую базу. Здесь будут обсуждаться две задачи. Первая достаточно простая, но не совсем привычная своей формулировкой, больно уж много там различных вводных. И поэтому ставящая детей в тупик. Зато появляется хороший повод обсудить с ребятами цепочки ассоциаций, возникающие при анализе задачи, и соответствующую им теоретическую базу. И вторая задача вновь адресует нас к вписанной и описанной окружностям треугольника.
Если до этого мы обсуждали взаимодействие окружности с другими геометрическими объектами, то здесь посмотрим на взаимное положение двух окружностей. Вспомним внутреннее и внешнее касание. И, самое главное, проведем параллель между задачей на построение и расчетной задачей, возвращаясь к идее о важности и полезности задач на построение. Мы увидим, как осмысленное построение общей внешней касательной к двум касающимся друг друга окружностям помогает как бы «изнутри» понять, как же найти длину отрезка этой общей касательной. Откуда там берется прямоугольник, или прямоугольный треугольник. Почему возникает разность радиусов, и так далее. Расчетная задача перестает быть технической, формульной. И становится эстетической.
Это последний урок курса, на котором мы, в некотором роде, подведем итоги. И сделаем это первыми двумя задачами, продолжающими линейку взаимодействий окружностей друг с другом и общими касательными. Вспомним еще раз, как сравнение расстояния между центрами с суммой или разностью радиусов может дать нам полезную информацию о взаимном положении этих окружностей. Как это может помочь в построении и понимании свойств объектов. Увидим, как та же самая сумма или разность радиусов внезапно может дать длину катета прямоугольного треугольника. И, наконец, в Задачах 3 и 4 впервые появляется взаимодействие окружностей с четырехугольниками, как иллюстрация известных теорем о возможности вписать и описать около четырехугольника окружность. Эти две последние задачи курса адресуют нас к мысленному продолжению работы с построением циркулем и линейкой, как помощником в любом разделе геометрии.
Преподаватель математики
Выпускница ФМЛ 239
Выпускница кафедры экономической кибернетики СПбГУ
Окончила аспирантуру ЭМИ РАН
В течение 14 лет преподавала в СПбГУ и 10 лет в Академической Гимназии при СПбГУ (45 интернат).
Окончила музыкальную школу по классу фортепиано
Занималась элементами арт-терапии, в том числе психологией звуковосприятия и цветопостановки
В ФМЛ 30 работает с 2018 года
Счастливая мама троих детей